Giải Toán 9 Bài 2: Hệ hai phương trình bậc nhất hai ẩn

Giải Toán 9 Bài 2: Hệ hai phương trình bậc nhất hai ẩn, Giải bài tập SGK Toán 9 Tập 2 trang 11, 12 giúp các em học sinh lớp 9 xem gợi ý giải các bài tập của Bài

Giải Toán 9 Bài 2: Hệ hai phương trình bậc nhất hai ẩn giúp các bạn học sinh tham khảo cách giải, đối chiếu với lời giải hay chính xác phù hợp với năng lực của các bạn lớp 9.

Giải bài tập Toán 9 trang 11, 12 tập 2 được biên soạn đầy đủ tóm tắt lý thuyết, trả lời các câu hỏi phần bài tập cuối bài. Qua đó giúp các bạn học sinh có thể so sánh với kết quả mình đã làm, củng cố, bồi dưỡng và kiểm tra vốn kiến thức của bản thân. Vậy sau đây là nội dung chi tiết giải bài tập Toán 9 bài 2 tập 2, mời các bạn cùng theo dõi tại đây.

Xem Tắt

1 Lý thuyết Hệ hai phương trình bậc nhất hai ẩn
2 Trả lời câu hỏi Toán 9 Bài 2
- 2.1 Câu hỏi trang 8
- 2.2 Câu hỏi trang 9
3 Giải bài tập Toán 9 trang 11 tập 2
4 Giải bài tập toán 9 trang 11 tập 2: Luyện tập

Lý thuyết Hệ hai phương trình bậc nhất hai ẩn

1. Khái niệm về hệ phương trình bậc nhất hai ẩn

+ Khái niệm: Hệ hai phương trình bậc nhất hai ẩn có dạng: $(I) left{begin{matrix} ax + by = c & & \ a'x + b'y = c' & & end{matrix}right.$

trong đó ax + by = c và a’x + b’y = c’ là những phương trình bậc nhất hai ẩn.

+ Nếu hai phương trình của hệ có nghiệm chung thì nghiệm chung ấy gọi là nghiệm của hệ phương trình (I). Trái lại, nếu hai phương trình không có nghiệm chung thì ta nói hệ (I) là vô nghiệm.

Giải hệ phương trình là tìm tất cả các nghiệm của nó.

2. Minh họa hình học tập nghiệm của hệ phương trình bậc nhất hai ẩn

Đối với hệ phương trình (I), ta gọi (d) là đường thẳng biểu diễn tập nghiệm của phương trình ax + by = c và (d’) là đường thẳng biểu diễn tập nghiệm của phương trình a’x + b’y = c’.

+ Nếu (d) cắt (d’) thì hệ (I) có một nghiệm duy nhất.

+ Nếu (d) song song với (d’) thì hệ (I) vô nghiệm.

+ Nếu (d) trùng với (d’) thì hệ (I) có vô số nghiệm.

3. Hệ phương trình tương đương

Hai hệ phương trình được gọi là tương đương với nhau nếu chúng có cùng tập nghiệm.

Ta dùng kí hiệu “⇔” để chỉ sự tương đương của hai hệ phương trình.

Trả lời câu hỏi Toán 9 Bài 2

Câu hỏi trang 8

Xét hai phương trình bậc nhất hai ẩn 2x+y=3 và x-2y=4.

Kiểm tra rằng cặp số (x; y) = (2; -1) vừa là nghiệm của phương trình thứ nhất, vừa là nghiệm của phương trình thứ hai.

+ Cặp số $(x_0;y_0)$ là nghiệm của phương trình ax+by=c khi $(x_0;y_0)$ thỏa mãn hệ thức $ax_0+by_0=c$

Lời giải chi tiết

+ Thay x=2;y=-1 vào phương trình 2x + y = 3 ta được 2.2 + (-1) = 3 $Leftrightarrow 3=3$ (luôn đúng)

$Rightarrow$ cặp số (x; y) = (2; -1) là nghiệm của phương trình 2x + y = 3

+ Thay x=2;y=-1 vào phương trình x – 2y = 4 ta được 2 – 2 .(-1) = 4 $Leftrightarrow$ 4=4 (luôn đúng)

$Rightarrow$ cặp số (x; y) = (2; -1) là nghiệm của phương trình x – 2y = 4

Vậy cặp số (x; y) = (2; -1) vừa là nghiệm của phương trình thứ nhất, vừa là nghiệm của phương trình thứ hai.

Câu hỏi trang 9

Tìm từ thích hợp để điền vào chỗ trống (…) trong câu sau:

Nếu điểm M thuộc đường thẳng ax + by = c thì tọa độ (x_o; y_o) của điểm M là một … của phương trình ax + by = c.

Lời giải chi tiết

Nếu điểm M thuộc đường thẳng ax + by = c thì tọa độ (x_o; y_o) của điểm M là một nghiệm của phương trình ax + by = c.

Giải bài tập Toán 9 trang 11 tập 2

Bài 4 (trang 11 SGK Toán 9 Tập 2)

Không cần vẽ hình, hãy cho biết số nghiệm của mỗi hệ phương trình sau đây và giải thích vì sao:

a) $left{begin{matrix} y = 3 - 2x & & \ y = 3x - 1 & & end{matrix}right.;$

b) $left{begin{matrix} y = -dfrac{1}{2}x+ 3 & & \ y = -dfrac{1}{2}x + 1 & & end{matrix}right.$

c) $left{begin{matrix} 2y = -3x & & \ 3y = 2x & & end{matrix}right.$

d) $left{begin{matrix} 3x - y = 3 & & \ x - dfrac{1}{3}y = 1 & & end{matrix}right.$

Xem gợi ý đáp án

a) Ta có:

$left{begin{matrix} y = 3 - 2x & & \ y = 3x - 1 & & end{matrix}right. ⇔ left{begin{matrix} y = -2x + 3 , (d) & & \ y = 3x - 1 , (d') & & end{matrix}right.$

Ta có a = -2, a’ = 3 nên a ≠ a’.

Do đó hai đường thẳng (d) và (d’) cắt nhau nên hệ phương trình đã cho có một nghiệm duy nhất.

b) Ta có:

$left{begin{matrix} y = -dfrac{1}{2}x+ 3 , (d) & & \ y = -dfrac{1}{2}x + 1 , (d') & & end{matrix}right.$

Ta có $a = -dfrac{1}{2},b = 3$ và $a' = -dfrac{1}{2}, b' = 1$ nên a = a’, b ≠ b’.

Do đó hai đường thẳng (d) và (d’) song song nên hệ phương trình đã cho vô nghiệm.

c) Ta có:

$left{begin{matrix} 2y = -3x & & \ 3y = 2x & & end{matrix}right.⇔ left{begin{matrix} y = -dfrac{3}{2}x , (d) & & \ y = dfrac{2}{3}x, (d') & & end{matrix}right.$

Ta có $a = -dfrac{3}{2}, a' = dfrac{2}{3}$ nên a ≠ a’

Do đó hai đường thẳng (d) và (d’) cắt nhau nên hệ phương trình đã cho có một nghiệm duy nhất.

d) Ta có:

$left{begin{matrix} 3x - y = 3 & & \ x - dfrac{1}{3}y = 1 & & end{matrix}right. ⇔left{begin{matrix} y = 3x - 3 & & \ dfrac{1}{3}y = x - 1 & & end{matrix}right. ⇔ left{begin{matrix} y = 3x - 3, (d) & & \ y = 3x - 3 , (d')& & end{matrix}right.$

Ta có a = 3, b = -3 và a’ = 3, b’ = -3 nên a = a’, b = b’.

Do đó hai đường thẳng (d) và (d’) trùng nhau nên hệ phương trình đã cho có vô số nghiệm.

Bài 5 (trang 11 SGK Toán 9 Tập 2)

Đoán nhận số nghiệm của hệ phương trình sau bằng hình học:

a) $left{ matrix{2{rm{x}} - y = 1 hfill cr x - 2y = - 1 hfill cr} right. ;$

b) $left{ matrix{2{rm{x + }}y = 4 hfill cr - x + y = 1 hfill cr} right.$

Xem gợi ý đáp án

a) Ta có:

$left{ matrix{ 2x - y = 1 hfill cr x - 2y = - 1 hfill cr} right. Leftrightarrow left{ matrix{ y = 2x - 1 (d)hfill cr y = dfrac{1}{2}x + dfrac{1}{2} (d') hfill cr} right.$

+) Vẽ (d): y=2x-1

Cho x = 0 ⇒ y = -1, ta được A(0; -1).

Cho $y = 0 Rightarrow x = dfrac{1}{2}$ , ta được $B{left(dfrac{1}{2}; 0 right)}$ .

Đường thẳng (d) là đường thẳng đi qua hai điểm A, B.

+) Vẽ (d’): $y=dfrac{1}{2}x+dfrac{1}{2}$

Cho x = 0 $Rightarrow y = dfrac{1}{2}$ , ta được $C {left(0; dfrac{1}{2} right)}.$

Cho y = 0 ⇒ x = -1, ta được D = (-1; 0).

Đường thẳng (d’) là đường thẳng đi qua hai điểm C, D.

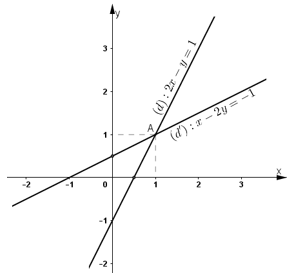
+) Quan sát hình vẽ, ta thấy hai đường thẳng cắt nhau tại điểm có tọa độ M( 1, 1).

Thay x = 1, y = 1 vào các phương trình của hệ ta được:

$left{ begin{array}{l}2x - y = 1\x - 2y = - 1end{array} right.$

$Rightarrowleft{ begin{array}{l}2.1 - 1 = 1\1 - 2.1 = - 1end{array} right. Leftrightarrow left{ begin{array}{l}1 = 1\ - 1 = - 1end{array} right.$ (luôn đúng)

Vậy hệ phương trình có một nghiệm (x; y) = (1; 1).

b) Ta có:

$left{ matrix{ 2x + y = 4 hfill cr - x + y = 1 hfill cr} right. Leftrightarrow left{ matrix{ y = - 2x + 4 (d) hfill cr y = x + 1 (d') hfill cr} right.$

+) Vẽ (d): y=-2x+4

Cho x = 0 ⇒ y = 4, ta được A(0; 4).

Cho y = 0 ⇒ x = 2, ta được B(2; 0).

Đường thẳng (d) là đường thẳng đi qua hai điểm A, B.

Vẽ (d’): y=x+1

Cho x = 0 ⇒ y = 1, ta được C(0; 1).

Cho y = 0 ⇒ x = -1, ta được D(-1; 0).

Đường thẳng (d’) là đường thẳng đi qua hai điểm C, D.

Quan sát hình vẽ, ta thấy hai đường thẳng cắt nhau tại điểm có tọa độ N(1;2).

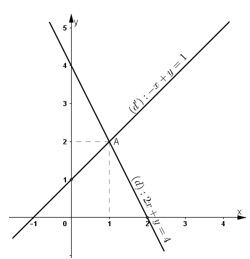Thay x = 1, y = 2 vào các phương trình của hệ ta được:

$left{ begin{array}{l}2x + y = 4\ - x + y = 1end{array} right. Rightarrow left{ begin{array}{l}2.1 + 2 = 4\ - 1 + 2 = 1end{array} right. Leftrightarrow left{ begin{array}{l}4 = 4\1 = 1end{array} right.$ (luôn đúng)

Vậy hệ phương trình có một nghiệm (x; y) = (1; 2).

Bài 6 (trang 11 SGK Toán 9 Tập 2)

Đố: Bạn Nga nhận xét: Hai hệ phương trình bậc nhất hai ẩn vô nghiệm thì luôn tương đương với nhau.

Bạn Phương khẳng định: Hai hệ phương trình bậc nhất hai ẩn cùng có vô số nghiệm thì cũng luôn tương đương với nhau.

Theo em, các ý kiến đó đúng hay sai? Vì sao? (Có thể cho một ví dụ hoặc minh họa bằng đồ thị).

Xem gợi ý đáp án

Bạn Nga đã nhận xét đúng vì hai hệ phương trình cùng vô nghiệm có nghĩa là chúng cùng có tập nghiệm bằng $S=phi$ (rỗng).

Bạn Phương nhân xét sai. Chẳng hạn, hai hệ phương trình:

$(I) left{begin{matrix} y = x & & \ y = x & & end{matrix}right. và (II) left{begin{matrix} y = -x & & \ y = -x & & end{matrix}right.$

Hệ (I) và hệ (II) đều có vô số nghiệm nhưng tập nghiệm của hệ (I) được biểu diễn bởi đường thẳng y = x, còn tập nghiệm của phương trình (II) được biểu diễn bởi đường thẳng y = -x. Hai đường thẳng này là khác nhau nên hai hệ đang xét không tương đương (vì không có cùng tập nghiệm).

Giải bài tập toán 9 trang 11 tập 2: Luyện tập

Bài 7 (trang 12 SGK Toán 9 Tập 2)

Cho hai phương trình 2x + y = 4 và 3x + 2y = 5.

a) Tìm nghiệm tổng quát của mỗi phương trình trên.

b) Vẽ các đường thẳng biểu diễn tập nghiệm của hai phương trình trong mỗi một hệ trục tọa độ, rồi xác định nghiệm chung của chúng.

Xem gợi ý đáp án

a) Ta có:

+) $2x{rm{ }} + {rm{ }}y{rm{ }} = {rm{ }}4{rm{ }} Leftrightarrow {rm{ }}y{rm{ }} = {rm{ }} - 2x{rm{ }} + {rm{ }}4{rm{ }}.$

Do đó phương trình có nghiệm dạng tổng quát là:

$left{ matrix{x in R hfill cr y = - 2{rm{x}} + 4 hfill cr} right.$

+) $3x + 2y = 5 Leftrightarrow y = - dfrac{3}{2}x + dfrac{5}{2}.$

Do đó phương trình có nghiệm tổng quát như sau:

$left{ matrix{ x in Rhfill cr y = - dfrac{3}{2}x + dfrac{5}{2} hfill cr} right.$

b) +) Vẽ (d): y =-2x+ 4

Cho x = 0 ⇒ y = 4 được A(0; 4).

Cho y = 0 ⇒ x = 2 được B(2; 0).

Đường thẳng (d) là đường thẳng đi qua hai điểm A, B.

+) Vẽ (d’): $y =-dfrac{3}{2}x+dfrac{ 5}{2}$

Cho x = 0 $Rightarrow y = dfrac{5 }{2},$ ta được $M{left(0;dfrac{5}{2} right)}.$

Cho y = 0 $Rightarrow x = dfrac{5 }{3}$ , ta được $N {left( dfrac{5}{3};0 right)}.$

Đường thẳng (d’) là đường thẳng đi qua hai điểm M, N.

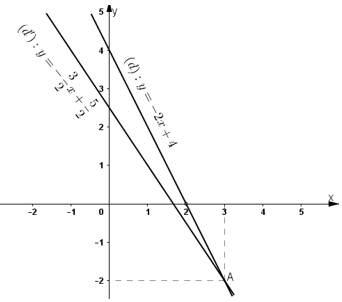
Hai đường thẳng cắt nhau tại D(3; -2).

Thay x = 3, y = -2 vào từng phương trình ta được:

2 . 3 + (-2) = 4 và 3 . 3 + 2 . (-2) = 5 (thỏa mãn)

Vậy (3; -2) là nghiệm chung của các phương trình đã cho.

Bài 8 (trang 12 SGK Toán 9 Tập 2)

Cho các hệ phương trình sau:

a) $left{ matrix{ x = 2 hfill cr 2x - y = 3 hfill cr} right.$

b) $left{ matrix{ x + 3y = 2 hfill cr 2y = 4 hfill cr} right.$

Xem gợi ý đáp án

a) Ta có

$left{ matrix{ x = 2 hfill cr 2x - y = 3 hfill cr} right. Leftrightarrow left{ matrix{ x = 2 (d) hfill cr y = 2x - 3 (d') hfill cr} right.$

Dự đoán: Hệ có nghiệm duy nhất vì một đồ thị là đường thẳng (d):x = 2 song song với trục tung, còn một đồ thị là đường thẳng (d’):y = 2x – 3 cắt hai trục tọa độ.

+) Vẽ (d): x = 2 là đường thẳng đi qua điểm có tọa độ (2;0) và song song với trục Oy.

+) Vẽ (d’ ): y =2x- 3

Cho x = 0 ⇒ y = -3 ta được A(0; -3).

Cho y = 0 $Rightarrow x = dfrac{3}{2}$ ta được $B{left(dfrac{3 }{2};0 right)}.$

Đường thẳng (d’) là đường thẳng đi qua hai điểm A, B.

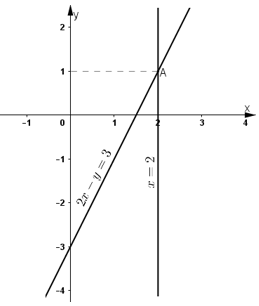
Ta thấy hai đường thẳng cắt nhau tại N(2; 1).

Thay x = 2, y = 1 vào hệ phương trình

$left{ begin{array}{l}x = 2\2x - y = 3end{array} right.$ ta được

$left{ begin{array}{l}2 = 2\2.2 - 1 = 3end{array} right. Leftrightarrow left{ begin{array}{l}2 = 2\3 = 3end{array} right.$ (luôn đúng)

Vậy hệ phương trình có nghiệm (2; 1).

b) $left{ matrix{ x + 3y = 2 hfill cr 2y = 4 hfill cr} right. Leftrightarrow left{ matrix{ y = - dfrac{1}{3}x + dfrac{2}{3}, (d)hfill cr y = 2 , (d') hfill cr} right.$

Hệ có nghiệm duy nhất vì một đồ thị là đường thẳng (d): $y = - dfrac{1 }{3}x + dfrac{2}{3}$ cắt hai trục tọa độ, còn một đồ thị là đường thẳng (d’):y = 2 song song với trục hoành.

+) Vẽ $y=-dfrac{1}{3}x+dfrac{2}{3}$

Cho x = 0 $Rightarrow y = dfrac{2}{3}$ ta được $A{left(0;dfrac{2}{3}right)} .$

Cho y = 0 ⇒ x = 2 ta được B(2; 0).

Đồ thị hàm số $y=-dfrac{1}{3}x+dfrac{2}{3}$ là đường thẳng đi qua hai điểm A, B.

+) Vẽ y = 2 là đường thẳng đi qua điểm có tọa độ (0;2) trên trục tung và song song với trục hoành (Ox)

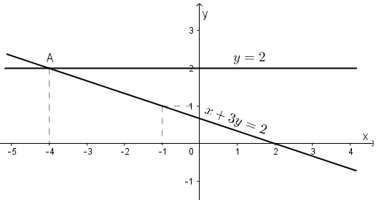
Ta thấy hai đường thẳng cắt nhau tại M(-4; 2).

Thay x = -4, y = 2 vào hệ phương trình

$left{ begin{array}{l}x+3y = 2\2y = 4end{array} right.$ ta được

$left{ begin{array}{l} - 4 + 3.2 = 2\2.2 = 4end{array} right. Leftrightarrow left{ begin{array}{l}2 = 2\4 = 4end{array} right.$ (luôn đúng)

Vậy hệ phương trình có nghiệm (-4; 2).

Bài 9 (trang 12 SGK Toán 9 Tập 2)

Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:

a) $left{begin{matrix} x + y = 2 & & \ 3x + 3y = 2 & & end{matrix}right.;$

b) $left{begin{matrix} 3x -2 y = 1 & & \ -6x + 4y = 0 & & end{matrix}right.$

Xem gợi ý đáp án

a) Ta có:

$left{begin{matrix} x + y = 2 & & \ 3x + 3y = 2 & & end{matrix}right. Leftrightarrow left{begin{matrix} y = -x + 2 & & \ 3y = -3x+2 & & end{matrix}right.$

$Leftrightarrow left{begin{matrix} y = -x + 2 , (d) & & \ y = -x + dfrac{2}{3} , (d')& & end{matrix}right.$

Suy ra a = -1, a’ = -1; b = 2, $b' = dfrac{2}{3}$ nên a = a’, b ≠ b’.

Do đó hai đường thẳng (d) và (d’) song song nhau nên hệ đã cho vô nghiệm.

b) Ta có:

$left{begin{matrix} 3x -2 y = 1 & & \ -6x + 4y = 0 & & end{matrix}right. Leftrightarrow left{begin{matrix} 2y = 3x - 1 & & \ 4y = 6x& & end{matrix}right.$

$Leftrightarrow left{begin{matrix} y = dfrac{3}{2}x - dfrac{1}{2} ,(d) & & \ y = dfrac{3}{2}x, (d')& & end{matrix}right.$

Ta có: $a = dfrac{3}{2}, a' = dfrac{3}{2}, b = -dfrac{1}{2}, b' = 0$ nên a = a’, b ≠b’.

Do đó hai đường thẳng (d) và (d’) song song với nhau nên hệ đã cho vô nghiệm.

Bài 10 (trang 12 SGK Toán 9 Tập 2)

Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:

a) $left{begin{matrix} 4x - 4y = 2 & & \ -2x + 2y = -1 & & end{matrix}right.$

b) $left{begin{matrix} dfrac{1}{3}x - y = dfrac{2}{3} & & \ x -3y = 2 & & end{matrix}right.$

Xem gợi ý đáp án

a. Ta có:

$left{begin{matrix} 4x - 4y = 2 & & \ -2x + 2y = -1 & & end{matrix}right. Leftrightarrow left{begin{matrix} 4y = 4x - 2 & & \ 2y = 2x - 1 & & end{matrix}right.$

$Leftrightarrow left{begin{matrix} y = x - dfrac{1}{2}, (d)& & \ y = x - dfrac{1}{2} , (d')& & end{matrix}right.$

Suy ra $a = a' = 1; b = b' = - dfrac{1}{2}.$

Do đó hai đường thẳng (d) và (d’) trùng nhau nên hệ phương trình có vô số nghiệm.

b)Ta có:

$left{begin{matrix} dfrac{1}{3}x - y = dfrac{2}{3} & & \ x -3y = 2 & & end{matrix}right.Leftrightarrow left{begin{matrix} y = dfrac{1}{3}x - dfrac{2}{3} & & \ 3y = x - 2 & & end{matrix}right.$

$Leftrightarrow left{begin{matrix} y = dfrac{1}{3}x - dfrac{2}{3} , (d)& & \ y = dfrac{1}{3}x - dfrac{2}{3} , (d')& & end{matrix}right.$

Suy ra $a = a' = dfrac{1}{3}, b = b' = -dfrac{2}{3}$

Do đó hai đường thẳng (d) và (d’) trùng nhau nên hệ phương trình có vô số nghiệm.

Bài 11 (trang 12 SGK Toán 9 Tập 2)

Nếu tìm thấy hai nghiệm phân biệt của một hệ hai phương trình bậc nhất hai ẩn (nghĩa là hai nghiệm được biểu diễn bởi hai điểm phân biệt) thì ta có thể nói gì về số nghiệm của hệ phương trình đó? Vì sao?

Xem gợi ý đáp án

Nếu một hệ phương trình bậc nhất hai ẩn có hai nghiệm phân biệt

⇒ Hệ đó có vô số nghiệm.

Vì hệ có hai nghiệm phân biệt nghĩa là hai đường thẳng biểu diễn tập nghiệm của hai phương trình của hệ có hai điểm chung phân biệt, suy ra chúng trùng nhau.