Toán lớp 5: Hình tam giác trang 85, Giải bài tập SGK Toán 5 trang 85, 86 giúp các em học sinh lớp 5 xem gợi ý giải các bài tập bài Hình tam giác của Chương 3 Toán
Giải Toán lớp 5: Hình tam giác giúp các em học sinh lớp 5 tham khảo, tổng hợp lại những kiến thức lý thuyết quan trọng, cùng đáp án 3 bài tập trong SGK Toán 5 trang 85, 86.
Thông qua bài viết này, các em sẽ củng cố lại kiến thức, rèn kỹ năng giải Toán 5 thật thành thạo. Đồng thời, cũng giúp thầy cô tham khảo để soạn giáo án bài Hình tam giác của Chương 3 Toán 5 cho học sinh của mình. Chi tiết mời thầy cô và các em cùng theo dõi bài viết dưới đây của Tài Liệu Học Thi:
Lý thuyết Hình tam giác
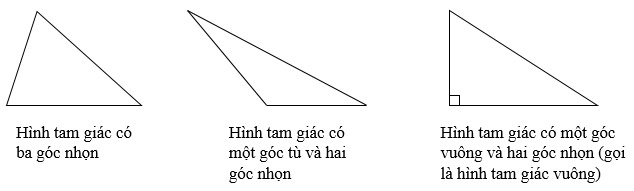
a) Hình tam giác
Hình tam giác ABC có:
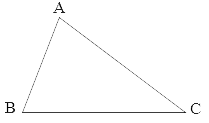
– Ba cạnh là: cạnh AB, cạnh AC, cạnh BC.
– Ba đỉnh là: đỉnh A, đỉnh B, đỉnh C.
– Ba góc là:
Góc đỉnh A, cạnh AB và AC (gọi tắt là góc A);
Góc đỉnh B, cạnh BA và BC (gọi tắt là góc B);
Góc đỉnh C, cạnh AC và CB (gọi tắt là góc C).
b) Đáy và đường cao
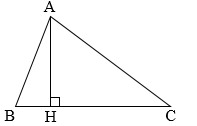
BC là đáy, AH là đường cao ứng với đáy BC. Độ dài AH là chiều cao.
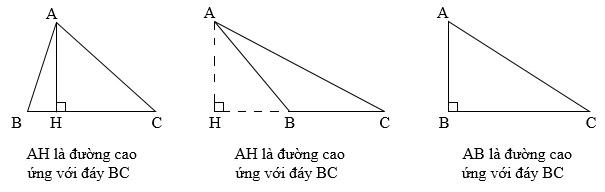
Giải bài tập Toán 5 trang 86
Bài 1
Viết tên ba góc và ba cạnh của mỗi hình tam giác dưới đây:
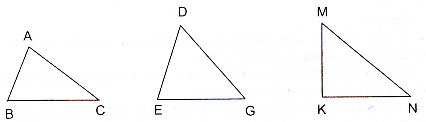
Gợi ý đáp án:
Viết tên 3 góc và 3 cạnh của hình tam giác:
Hình 1: Ba góc là góc A, góc B, góc C
Ba cạnh là: AB, BC, CA
Hình 2: Ba góc là góc D, góc E, góc G
Ba cạnh là: DE, EG, GD
Hình 3: Ba góc là góc M, góc K, góc N
Ba cạnh là: MK, KN, NM
Bài 2
Hãy chỉ ra đáy và đường cao tương ứng được vẽ trong mỗi hình tam giác dưới đây:

Gợi ý đáp án:
– Hình tam giác ABC: đáy là AB, đường cao tương ứng là CH.
– Hình tam giác DEG: đáy là EG, đường cao tương ứng là DK.
– Hình tam giác MPQ: đáy là PQ, đường cao tương ứng là MN.
Ngoài ra quan sát hình vẽ ta thấy tam giác MPQ là tam giác vuông tại M. Do đó ta có đáy và đường cao như sau:
+ Đáy là MQ, đường cao tương ứng là PM.
+ Đáy là PM, đường cao tương ứng là QM.
Bài 3
So sánh diện tích của:
a) Hình tam giác AED và hình tam giác EDH
b) Hình tam giác EBC và hình tam giác EHC
c) Hình chữ nhật ABCD và hình tam giác EDC
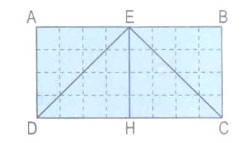
Gợi ý đáp án:
So sánh diện tích của
a) Diện tích tam giác AED = diện tích tam giác EDH
b) Diện tích tam giác EBC = diện tích tam giác EHC
c) Diện tích chữ nhật ABCD = 2 lần diện tích tam giác EDC










