Cách chứng minh tam giác vuông

Chứng minh tam giác vuông là tài liệu vô cùng hữu ích mà Tài Liệu Học Thi muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 9 tham khảo.

Tài liệu tổng hợp toàn bộ kiến thức về khái niệm, dấu hiệu nhận biết, cách dựng tam giác vuông, tính chất, cách chứng minh và một số bài tập có đáp án kèm theo. Thông qua tài liệu này các bạn có thêm nhiều gợi ý ôn tập, củng cố kiến thức, nắm được cách chứng minh tam giác vuông để giải các bài tập Toán 9. Bên cạnh đó các bạn tham khảo thêm Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức chứa dấu căn.

I. Tam giác vuông là gì?

– Tam giác vuông là tam giác có một góc bằng 90⁰

Ví dụ: Cho tam giác ABC vuông tại B, ta có hình vẽ minh họa như sau:

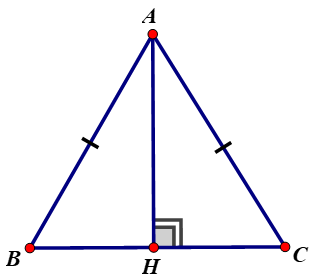
II. Dấu hiệu nhận biết tam giác vuông

• Tam giác có một góc vuông là tam giác vuông
• Tam giác có hai góc nhọn phụ nhau là tam giác vuông
• Tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia là tam giác vuông
• Tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy là tam giác vuông
• Tam giác nội tiếp đường tròn có một cạnh là đường kính của đường tròn là tam giác vuông

III. Cách dựng tam giác ABC vuông tại A

Cho trước cạnh huyền BC = 4,5 cm và cạnh góc vuông AC = 2 cm.

– Dựng đoạn AC = 2 cm

– Dựng góc CAx bằng 90^o.

– Dựng cung tròn tâm C bán kinh 4,5 cm cắt Ax tại B. Nối BC ta có Δ ABC cần dựng.

IV. Tính chất của tam giác vuông

Tính chất 1: Trong tam giác vuông, hai góc nhọn phụ nhau.

Định lý Pitago

Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

Định lý Pitago đảo

Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh còn lại thì tam giác đó là tam giác vuông.

Tính chất 3: Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.

V. Các cách chứng minh tam giác vuông

Có tất cả 5 cách chứng minh tam giác vuông như sau:

• Chứng minh tam giác có một góc bằng 90 độ
• Chứng minh tam giác có tổng hai góc nhọn bằng 90 độ
• Chứng minh tam giác có bình phương độ dài một cạnh bằng tổng bình phương độ dài hai cạnh kia. Áp dụng định lý Pitago.
• Chứng minh tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy.
• Chứng minh tam giác nội tiếp một nửa đường tròn (có 1 cạnh trùng đường kính).

Cách 1: Để chứng minh một tam giác là tam vuông ta chứng minh tam giác đó có tổng 2 góc nhọn bằng 90 độ (2 góc nhọn phụ nhau).

Ví dụ 1: Tam giác ABC có góc B + C = 90°

⇒ Tam giác ABC vuông tại A.

* Cách 2: Để chứng minh một tam giác là tam vuông ta chứng minh tam giác đó có bình phương độ dài một cạnh bằng tổng bình phương độ dài hai cạnh kia.

Ví dụ 2: Tam giác ABC có AB² + AC² = BC²

⇒ Tam giác ABC vuông tại A.

* Cách 3: Để chứng minh một tam giác là tam vuông ta chứng minh tam giác đó có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy.

Ví dụ 3: Tam giác ABC có M là trung điểm BC, biết AM = MB = MC = ½ BC

=> Tam giác ABC vuông tại A.

* Cách 4: Chứng minh tam giác có một góc bằng 90 độ.

+ Cách làm: Đưa góc cần chứng minh vào góc của một tứ giác rồi chứng minh tứ giác đó là hình chữ nhật, hình vuông, hoặc góc tạo bởi 2 đường chéo của hình thoi, hình vuông.

* Cách 5: Để chứng minh một tam giác là tam vuông ta chứng minh tam giác đó nội tiếp đường tròn và có một cạnh là đường kính.

Ví dụ 4: Tam giác OAB nội tiếp đường tròn đường kính AB

=> Tam giác OAB vuông tại O.

VI. Bài tập chứng minh tam giác vuông

Câu 1

Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm.

a) Chứng minh tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH của tam giác đó.

b) Hỏi rằng điểm M mà diện tích tam giác MBC bằng diện tích tam giác ABC nắm trên đường nào?

Bài 2. Cho tam giác ABC có D, E thuộc cạnh BC sao cho BD = DE = EC. Biết AD = AE. Biết

a) Chứng minh

b) Gọi M là trung điểm của BC. Chứng minh AM là phân giác của

c) Giả sử . Tính các góc còn lai của tam giác DAE.

Bài 3. Cho tam giác ABC vuông ở A. TRên tia đối của tia AC lấy điểm D sao cho AD = AC.

a) Chứng minh DABC = DABD

b) Trên tia đối của tia AB, lấy điểm M. Chứng minh DMBD = D MBC.

Bài 4. Cho góc nhọn xOy và tia phân giác Oz của góc đó. Trên Ox, lấy điểm A, trên Oy lấy điểm B sao cho OA = OB. Trên tia Oz, lấy điểm I bất kì. Chứng minh:

a) D AOI = D BOI.

b) AB vuông góc OI..

Bài 5. Cho có . Kẻ tia phân giác của ( D thuộc BC). Trên canh AC lấy điểm E sao cho A E=A B, trên tia A B lấy điểm F sao cho A F=A C. Chứng minh rằng:

c) FDE thẳng hàng.