Định lí Py-ta-go

Định lí Py-ta-go, Định lí Py-ta-go bao gồm lý thuyết về Định lý Pitago, định lý Pitago đảo và các dạng bài tập. Thông qua tài liệu này giúp các bạn có thêm nhiều

Định lí Py-ta-go là mối liên hệ căn bản trong hình học Euclid giữa ba cạnh của một tam giác vuông. Vậy công thức tính định lí Pytago là gì? Mời các bạn cùng theo dõi bài viết dưới đây của Tài Liệu Học Thi nhé.

Trong bài viết hôm nay Tài Liệu Học Thi sẽ giới thiệu đến các bạn về định lý, công thức tính và các dạng bài tập kèm theo. Thông qua bài viết này các bạn có thêm nhiều kiến thức tham khảo để học tốt môn Toán lớp 7. Ngoài ra các bạn tham khảo thêm một số tài liệu khác như: tổng hợp kiến thức môn Toán lớp 7, tính chất trực tâm trong tam giác, Các trường hợp bằng nhau của hai tam giác và rất nhiều tài liệu khác tại chuyên mục Toán 7.

Xem Tắt

1 I. Lý thuyết Định lí Py-ta-go
2 II. Bài tập trắc nghiệm Định lí Py-ta-go
3 III. Bài tập tự luận Định lí Py-ta-go
4 IV. Bài tập tự luyện định lý Pitago

I. Lý thuyết Định lí Py-ta-go

1. Định lý Pitago

Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

ΔABC vuông tại A ⇒ BC² = AB² + AC²

2. Công thức Pytago đảo

Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.

ΔABC có BC² = AB² + AC² ∠BAC = 90^o

II. Bài tập trắc nghiệm Định lí Py-ta-go

Bài 1: Cho tam giác ABC vuông tại B. Khi đó

A. AB² + BC² = AC²

B. AB² – BC² = AC²

C. AB² + AC² = BC²

D. AB² = AC² + BC²

Ta có tam giác ABC vuông tại B, theo định lí Py – ta – go ta có: AB² + BC² = AC²

Chọn đáp án A.

Bài 2: Cho tam giác ABC vuông cân tại A. Tính độ dài cạnh BC biết AB = AC = 2dm

A. BC = 4 dm B. BC = √6 dm C. BC = 8dm D. BC = √8 dm

Áp dụng định lí Py – ta – go ta có: BC² = AB² + AC²

Khi đó ta có:

$B C=sqrt{A B^{2}+A C^{2}}=sqrt{4+4}=sqrt{8}(d m)$

Chọn đáp án D.

Bài 3: Một tam giác vuông có cạnh huyền bằng 26cm và có độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông?

A. 10 cm, 22 cm B. 10 cm, 24 cm C. 12 cm, 24 cm D. 15 cm, 24 cm

Gọi độ dài các cạnh góc vuông lần lượt là x, y (x, y > 0)

Theo định lí Py – ta – go ta có: x² + y² = 26² ⇔ x² + y² = 676

Theo bài ra ta có:

$frac{x}{5}=frac{y}{12} Rightarrow frac{x^{2}}{25}=frac{y^{2}}{144}=frac{x^{2}+y^{2}}{25+144}=frac{676}{169}=4$

Khi đó ta có:

$left{begin{array}{l}x^{2}=25.4 \ y^{2}=144.4end{array} Rightarrowleft{begin{array}{l}x=10 mathrm{~cm} \ x=24 mathrm{~cm}end{array}right.right.$

Chọn đáp án B.

Bài 4: Cho tam giác ABC vuông tại A có AC = 20cm. Kẻ AH vuông góc với BC. Biết BH = 9cm, HC = 16cm. Tính độ dài cạnh AB, AH ?

A. AH = 12cm, AB = 15cm

B. AH = 10cm, AB = 15cm

C. AH = 15cm, AB = 12cm

D. AH = 12cm, AB = 13cm

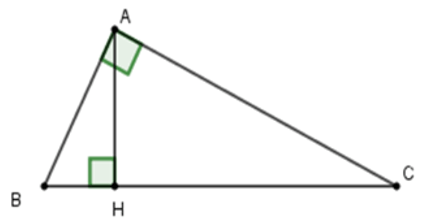
Ta có: BC = HB + HC = 9 + 16 = 25 (cm)

Xét tam giác ABC vuông tại A, theo định lí Py – ta – go ta có:

BC² = AB² + AC² ⇒ AB² = BC² – AC² = 25² – 20² = 225 ⇒ AB = 15cm

Xét tam giác ABH vuông tại H, theo định lí Py – ta – go ta có:

HB² + HA² = AB² ⇒ AH² = AB² – HB² = 15² – 9² = 144 ⇒ AH = 12cm

Vậy AH = 12cm, AB = 15cm

Chọn đáp án A.

Bài 5: Cho hình vẽ. Tính x

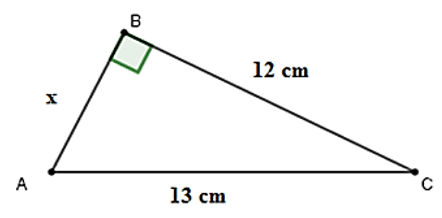
A. x = 10cm B. x = 11cm C. x = 8cm D. x = 5cm

Xét tam giác ABC vuông tại B ta có:

⇒ x² + 12² = 13² ⇒ x² = 13² – 12² = 25

Khi đó: x = 5cm

Chọn đáp án D.

III. Bài tập tự luận Định lí Py-ta-go

Câu 1

Tìm độ dài x trên hình 127.

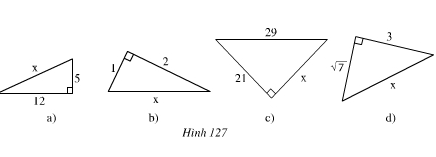
Giải

– Hình a

Áp dụng định lí Pi-ta-go ta có:

x² = 12² + 5² = 144 + 25 = 169 ⇒ x = 13

– Hình b

Ta có: x² = 1² + 2² = 1 + 4 = 5

⇒ x = √5

Hình c

Theo định lí Pi-ta-go 29² = 21² + x²

Nên x² = 29² – 21² = 841 – 441 = 400

⇒ x = 20

– Hình d

Theo định lí Pi-ta-go ta có:

x² = (√7)² + 3² = 7 + 9 = 16

⇒ x = 4

Câu 2. Đoạn lên dốc từ C đến A dài 8,5m, độ dài CB bằng 7,5m. Tính chiều cao AB.

Vẽ hình minh họa:

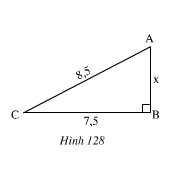
Áp dụng định lí Py–ta–go vào tam giác vuông ABC vuông tại B ta có:

AB² + BC² = AC²

Nên AB² = AC² – BC²

= 8,5² – 7,5²

= 72,25 – 56,25

=16

⇒ AB = 4 (m)

Câu 3: Tính chiều cao của bức tường, biết rằng chiều dài của thang là 4m và chân thang cách tường 1m

Giải

Vẽ hình minh họa:

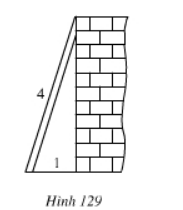
Kí hiệu như hình vẽ:

Vì mặt đất vuông góc với chân tường nên góc C = 90º.

Áp dụng định lí Pi-ta-go trong ΔABC ta có:

AC² + BC² = AB²

⇒ AC² = AB² – BC² = 16 – 1 = 15

⇒ AC = √15 ≈ 3,87(m) hay chiều cao của bức tường là 3,87m.

Câu 4. Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau.

a) 9cm, 15cm, 12cm.

b) 5dm, 13dm, 12dm.

c) 7m, 7m, 10m.

Giải

a) Ta có 9² = 81 ; 15² =225 ; 12² =144

Mà 225 = 144 + 81

Nên Theo định lí Py – ta – go đảo, tam giác có độ dài 3 cạnh 9cm ,12cm ,15cm là tam giác vuông.

b) Ta có 5² = 25 ; 13² =169 ; 12² =144

Mà 169 = 144 + 25

Nên Theo định lí Py – ta – go đảo tam giác có độ dài 3 cạnh 5dm ,13dm ,12dm là tam giác vuông.

c) Ta có 7² = 49 ; 10² =100

Mà 100 ≠ 49 + 49

Nên tam giác có độ dài 3 cạnh 7m, 7m, 10m không là tam giác vuông

IV. Bài tập tự luyện định lý Pitago

Bài 1:

Cho DABC vuông tại A. biết AB + AC = 49cm; AB – AC = 7cm. Tính cạnh BC.

Bài 2:

Cho DABC vuông tại A. có BC = 26cm, AB:AC = 5:12. Tính độ dài AB và AC.

Bài 3:

Cho DABC vuông tại A. Kẻ đ ường cao AH. Biết BH = 18 cm; CH = 32cm. Tính các cạnh AB và AC.

Bài 4:

Cho DABC có AB = 9cm; AC = 11cm. Kẻ đường cao AH, bi ết BH = 26cm. Tính CH ?

Bài 5: Cho DABC vuông tại A. Kẻ AH vuông góc BC.

a/ Chứng minh: AB² + CH² = AC² + BH²

b/ Trên AB lấy E, trên AC lấy đi ểm F. Ch ứng minh: EF < BC.

c/ Bi ết AB = 6cm, AC = 8 cm. Tính AH, BH, CH.

Bài 6:

Cho DABC cân, AB = AC = 17cm. Kẻ BD vuông góc AC. Tính BC, biết BD = 15cm.

Bài 7: Cho DABC. Biết BC = 52cm, AB = 20cm, AC = 48cm.

a/ CM: DABC vuông ở A.

b/ Kẻ AH vuông góc BC. Tính AH.

Bài 8:

Hãy kiểm tra xem tam giác ABC có phải là tam giác vuông không nếu các cạnh AB, AC và BC tỉ lệ với:

a/ 9; 12 và 15 b/ 3; 2,4 và 1,8.

c/ 4; 6 và 7 d/ 4; 4 và 4.

Bài 9: Cho DABC vuông tại A, đường cao AH, trên đó lấy điểm D. Trên tia đối của tia HA lấy E sao cho HE = AD. Đường vuông góc với AH tại D cắt AC tại F.

Chứng minh rằng: EB vuông góc EF.

Bài 10: Cho góc nhọn xOy. Điểm H nằm trên tia phân giác của góc xOy. Từ H dựng các đường vuông góc xuống hai cạnh Ox và Oy (A thuộc Ox và B thuộc Oy).

a) Chứng minh tam giác HAB là tam giác cân

b) Gọi D là hình chiếu của điểm A trên Oy, C là giao điểm của AD với OH.

Chứng minh BC ⊥ Ox.

c) Khi góc xOy bằng 60⁰, chứng minh OA = 2OD.

Bài 11:

Cho tam giác ABC cân tại A. Gọi M, N là trung điểm các cạnh AB, AC. Các đường thẳng vuông góc với AB, AC tại M; N cắt nhau tại điểm O, AO cắt BC tại H. Chứng minh:

a. AMO = ANO

b. AH là phân giác của góc A

c. HB = HC và AH ⊥ BC

d. So sánh OC và HB

Bài 12: Cho tam giác cân ABC (AB = AC). Từ trung điểm M của BC vẽ ME ⊥ AC và MF ⊥AC. Chứng minh:

a. BEM = CFM

b. AE = AF

c. AM là phân giác của góc EMF

d. So sánh MC và ME

Bài 13: Cho tam giác ABC có = 90⁰ , AB = 8cm, AC = 6cm .

a. Tính BC .

b. Trên cạnh AC lấy điểm E sao cho AE = 2cm; trên tia đối của tia AB lấy điểm D sao cho AD = AB. Chứng minh ∆BEC = ∆DEC .